Úvod
To jsem takhle jednou šel na hnojárně ústavem matematiky a na co jsem nenarazil než na kupu knih s nápisem 'K ROZEBRÁNÍ' - ústav se zbavoval nepotřebné literatury. Samozřejmě jsem si řekl, že si musím nějaké to moudro odnést - co dnes člověk dostane zadarmo? Chvíli jsem váhal mezi infinitezimálním počtem v azbuce a sbírkou Schwierige Rechenaufgaben z roku 1935, ale nakonec mi do oka padla útlá brožurka vydaná v Polytechnické knižnici a nazvaná Počítáme na logaritmickém pravítku. Ihned jsem zatoužil zacelit citelnou mezeru ve svém vzdělání a naučit se ovládat tuto extrémně vymakanou babičku kalkulaček a podobných zařízení. Proto kniha změnila majitele a já vám nyní mohu předložit její stručný elaborát, čímž doufám získám další desítky příznivců tohoto originálního a k přírodě zaručeně šetrného (nepotřebuje žádné baterie) způsobu počítání.
Popis Pravítka
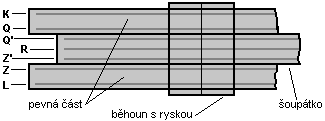
Nejsnázeji je učit se na univerzálním typu pravítka, uspořádaného podle systému Rietzova. To u nás produkovala firma Logarex v různě dlouhých provedeních - 100, 250 a 500 mm. Logaritmické pravítko se skládá za tří částí:
- pevná (základní) část
- pohyblivá část (šoupátko) která se posunuje v drážkách pevné části
- průhledný běhoun s ryskou

- úplně nejníž a začátečníkovi nejznámější je rovnoměrná stupnice v milimetrech
- na horním okraji dolní pevné části je tzv. základní logaritmická stupnice Z
- identická stupnice - Z' je i na dolní části běhounu - s dvojicí stupnic Z a Z' budeme pracovat nejdříve
- uprostřed běhounu je stupnice reciproká, nadepsaná 1/X, označovaná též R
- na horní hraně běhounu pak nalezneme stupnici X 2 - kvadratickou - Q
- opět stejná stupnice Q' je i na dolní hraně horního pruhu hlavní části
- výčet stupnic pak uzavírá stupnice kubická - K
Konstrukce logaritmické stupnice
Pro začátečníky - logaritmus čísla x při základu n je číslo, na které musíme základ n umocnit abychom dostali číslo x.
Základem stupnice je logaritmus o základu 10. Počátek stupnice označený 1 je log(1) = 0 a konec, označený 10 , tvoří logaritmus 10 tedy 1. Prostor mezi těmito čísly je vyplněn kótami 2,3,...,9, které odpovídají dekadickým logaritmům jednotlivých čísel. Z vlastností logaritmů pak plyne na první pohled patrná nerovnoměrnost stupnice. Jeden příklad: Pod značkou 3 se zkrývá délka logaritmu trojky. Protože log(3) = 0,47712 leží značka ve vzdálenosti rovné 0,47712-násobku základní délky 1-10 odpovídající logaritmu 10 (tedy zhruba v polovině stupnice. Prostor mezi logaritmy celých čísel je rozdělen na dílky jejichž jemnost se vzrůstajícím číslem klesá - mezi 1 a 2 je stupnice po 0,01 , poslední úsek 9-10 je rozdělen již jen na desetiny. Na stejném principu jsou konstruovány i obě stupnice kvadratické Q, Q', kubická K i reciproká R.
Násobení
Po letmém osvětlení konstrukce přístroje přistupme k prvnímu a nejjednoduššímu početnímu úkonu na pravítku - násobení. Potřebovat k němu budeme zatím jen základní logaritmické stupnice Z, Z'. Princip násobení vyjadřuje následující vztah
Nejde tedy o nic jiného, než že sečteme dvě úsečky o délkách odpovídajících logaritmům příslušných čísel. Je patrno, že na pravítku máme k dispozici pouze logaritmy čísel 1 - 10. Čísla proto musíme převádět do tvaru mantisa + exponent (1548 = 1,548 * 103) a odděleně vypočítat mantisu výsledku na pravítku a řád exponentu v hlavě.
V zásadě se násobení dvou čísel a, b, pro která platí 1 < a < 10 rozpadá na dva případy
a) a*b<10
Postup:- Rysku běhounu nastavíme nad kótu čísla a na stupnici Z
- Pod rysku nastavíme kótu 1 stupnice Z'
- Běhoun posuneme nad kótu čísla b na stupnici Z'
- Pod ryskou běhounu čteme na stupnici Z kótu výsledku a*b
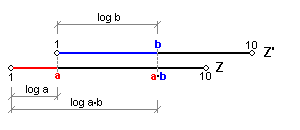
Z obrázku je patrné, jak jsme sečetli dvě úsečky délky log(a), log(b)ve výslednou log(a*b)
b) a*b>10
Složitější situace nastane pokud překročí součin desítku. Stupnice logaritmů totiž končí log 10. Pomůžeme si tak že číslo a nejprve vydělíme 10 a potom teprve násobíme b. Postup je následující:
- Nad kótu čísla a na stupnici Z nastavíme kótu 10 stupnice Z'. Šoupátko se posunuje doleva.
- Rysku běhounu se nastaví nad kótu b na stupnici Z' a pod ní odečteme na Z kótu výsledku odpovídajícího číslo a*b/10. Odečtený výsledek tedy musíme násobit 10.
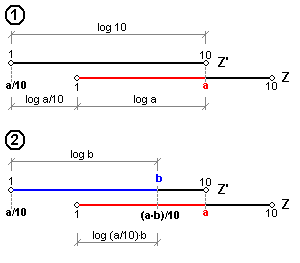
Z obrázku vyplývá, že od úsečky o délce log(a) jsme odečetli log(10) (tj provedli jsme a/10). Tak jsme se dostali mimo stupnici Z doleva. Na ni jsme se vrátili přičtením úsečky délky log(b).
což odpovídá:
a/10 * b
Dělení
Dělení je operací opačnou k násobení, a proto je postup analogický k násobení. Tentokrát však nebudeme logaritmy jednotlivých činitelů sčítat, ale odčítat podle vztahu:
Opět nastanou dvě možnosti postupu v závislosti na vzájemné velikosti čitatele (dělence) a a jmenovatele (dělitele) b
a) a>b
V tomto jednodušším případě se jedná o postup zcela opačný výše uvedenému násobení a*b , kdy a*b<10.
Postup:- Rysku běhounu nastavíme nad kótu čísla a na stupnici Z
- Pod rysku nastavíme kótu čísla b na stupnici Z'
- Běhoun posuneme nad kótu 1 na stupnici Z'
- Pod ryskou běhounu čteme na stupnici Z kótu výsledku a/b
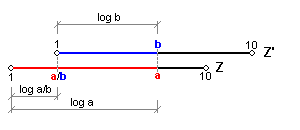
b) a < b
Pokud dodržujeme výše zmíněný postup dělení i v případě, kdy je dělitel větší než dělenec, nemůžeme odečítat výsledek přímo pod kótou 1 stupnice Z', protože šoupátko je vysunuto doleva a kóta 1 je mimo stupnici Z. Proto výsledek vynásobíme 10. To, jak už víme, znamená na logaritmickém pravítku připočtení úsečky délky celé stupnice 1-10. Výsledek tedy dostanem 10x větší.
Postup:- Nad kótu dělence a na stupnici Z nastavíme kótu dělitele b stupnice Z'. Šoupátko se posunuje doleva.
- Rysku běhounu se nastaví nad kótu 10 na stupnici Z' a pod ní odečteme na Z kótu výsledku odpovídajícího číslo (a/b)*10. Odečtený výsledek pak dělíme 10.
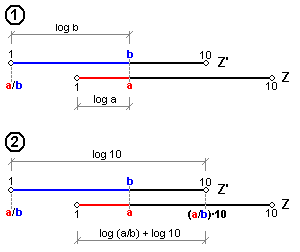
Je patrné, že příklady postupy dělení a násobení jsou v obou případech analogické.
Násobení a dělení na reciproké stupnici
Nyní se dostáváme k třetí stupnici pravítka, která je umístěna uprostřed posuvné části. Při bližším pohledu zjistíme, že tato stupnice je přesnou kopií základní logaritmické stupnice Z, avšak je otočena. Kótě 10 stupnice Z odpovídá kóta 1 stupnice R. Stupnice zobrazuje logaritmy čísel převrácených k číslům zákl. stupnice, tedy 1/2, 1/3, ... , 1/10. To jsou čísla menší než jedna a ty mají jak známo záporné logaritmy. To vysvětluje orientaci stupnice R zprava doleva. Kóta 1 odpovídá log(1/1) = 0 , kóta 3 odpovídá log(1/3) = -0.48 a tak dále - kóta 10 stupnice R je log(1/10) tedy -1.
Kdybychom tedy vysunuli pohyblivou část pravítka zcela doleva tak, aby se spolu kryly kóty 1 stupnic Z a R, dostali bychom vlastně stupnici logaritmů od -1 do 1, kdy zápornou část tvoří stupnice R a kladnou stupnice Z. Je důležité si uvědomit, že absolutní hodnoty logaritmu čísla a jeho převrácené hodnoty se rovnají. To snadno dokážeme užitím základních pravidel pro počítání z logaritmy:
Nyní se ale již podívejme na postup počítání, který je naprosto analogický k již uvedenému násobení a dělení. Opět se jedná o sčítání a odečítání úseček odpovídajících logaritmům operandů. Nepřipojuji tentokrát obrázky, neboť ten, kdo pochopil operace na základních stupnicích, je nebude potřebovat.
a) násobení a*b<10
- Rysku běhounu nastavíme nad kótu čísla a na stupnici Z
- Pod rysku nastavíme kótu čísla b na stupnici R
- Běhoun posuneme nad kótu 1 na stupnici R
- Pod ryskou běhounu čteme na stupnici Z kótu výsledku a*b
b) násobení a*b>10
- Rysku běhounu nastavíme nad kótu čísla a na stupnici Z
- Pod rysku nastavíme kótu čísla b na stupnici R
- Běhoun posuneme nad kótu 10 na stupnici R
- Pod ryskou běhounu čteme na stupnici Z kótu výsledku (a*b)/10
c) dělení a>b
- Rysku běhounu nastavíme nad kótu čísla a na stupnici Z
- Pod rysku nastavíme kótu 1 na stupnici R
- Běhoun posuneme nad kótu čísla b na stupnici R
- Pod ryskou běhounu čteme na stupnici Z kótu výsledku a/b
d) dělení a<b
- Rysku běhounu nastavíme nad kótu čísla a na stupnici Z
- Pod rysku nastavíme kótu 10 na stupnici R
- Běhoun posuneme nad kótu čísla b na stupnici R
- Pod ryskou běhounu čteme na stupnici Z kótu výsledku (a/b)*10
Je tedy patrné že násobení a dělení na základních stupnicích, či na základní a reciproké je shodné jak po stránce principu, tak co se týče počtu nutných úkonů. Záleží tedy hlavně na vašem subjektivním názoru, kterému způsobu dáte přednost. Mě osobně se lépe počítá se základními stupnicemi, protože k tomuto v podstatě nepotřebujete běhoun, zatímco při počítání se stupnicí R se bez něj neobejdete.